تكامل
في الرياضيات، مكاملة دالة هي نوع من التعميم لكميات قابلة للتجزئة مثل المساحة أو الحجم أو الكتلة أو أي مجموع لعناصر متناهية في الصغر. وأيضاً يمكن أن يُنظر إلى عملية التكامل على أنها عملية عكسية لعملية التفاضل. بالرغم من تعدد التعاريف المستخدمة للتكامل وتعدد طرق استخدامه فإن نتيجة هذه الطرق جميعها متشابهة وجميع التعاريف تؤدي في النهاية إلى المعنى ذاته.
| جزء من سلسلة مقالات حول |
| التفاضل والتكامل |
|---|
 |
| بوابة رياضيات |

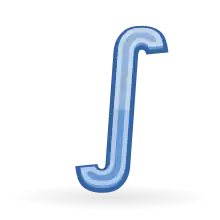
يمكن اعتبار تكامل دالة حقيقية مستمرة ذات قيم موجبة لمتغير حقيقي بين قيمة حدية دنيا وقيمة حدية عليا هي المساحة المحصورة بين المستقيمين الرأسيين: x=a, x=b والمحور x والمنحني المحدد بالدالة، يمكن صياغة ذلك بشكل رياضي:
ويرمز لهذه العملية حسب اصطلاح لورينتز:
.
النقطة الأساسية في التكامل تأتي من المبرهنة الأساسية في التكامل والتي تنص على أن مشتق تابع المساحة تحت منحني الدالة هو الدالة نفسها. بالتالي إذا عرفنا دالة تربط القيمة x بقيمة المساحة المحدودة بين منحني الدالة ومحور السينات (x) ومن الجهة الأخرى محدودة بمحور الصادات (y) والمستقيم X=x، تدعى هذه الدالة بدالة المساحة ومشتقها هو الدالة نفسها، لذلك ندعو تابع المساحة عكس الاشتقاق أو التابع الأصلي للدالة . يقوم حساب التكامل على إيجاد التابع الأصلي للدالة التي نريد القيام بمكاملتها.
وقد عرض غوتفريد لايبنتز، في 13 نوفمبر 1675، أول عملية تكامل لحساب المساحة تحت منحنى الدالة ص = د(س).
يوجد عدة أنواع للتكامل منها: التكامل بالتجزئة، تكامل بالتعويض، التكامل بالكسور الجزئية، التكامل بالأقراص.
تاريخ
التكامل ما قبل عصر علم التفاضل والتكامل
توجد دلالات تاريخية على استخدام التكامل في عهد قدماء المصريين (حوالي 1800 قبل الميلاد) فقد دلت بردية موسكو الرياضية على علمهم بصيغة لحساب حجم الهرم المقطوع. وتعد طريقة الاستنزاف من أوائل الطرق المستعملة في إيجاد التكاملات حيث تعود إلى 370 قبل الميلاد وكانت تحسب بها الحجوم والمساحات وذلك بتقسيمها إلى أشكال صغيرة غير منتهية معلومة المساحة أو الحجم. كما تم تطوير هذه الطريقة من قبل أرخميدس وتم استعمالها في حساب مساحات القطع المكافئ والتقريب لمساحة الدائرة. وفي الصين طورت طرق مماثلة في القرن الثالث الميلادي بواسطة ليو هوي، والذي استخدمها لإيجاد مساحة الدائرة كما تم استعمال هذه الطرق فيما بعد في القرن الخامس من قبل الرياضيين الصينيين - الأب والابن تسوتشونغ وزوجنغ [الإنجليزية] لإيجاد حجم الكرة.[1] في نفس القرن، استخدم الرياضي الهندي أريابهاتا طريقة مشابهة لحساب حجم المكعب.[2]
أتت الخطوة التالية والهامة في التفاضل التكاملي في القرن الحادي عشر عندما أخترع الفيزيائي الحسن بن الهيثم ما يعرف اليوم باسم مسألة الحسن (نسبة لاسمه المشهور عند الأوروبيين) والتي تقود إلى معادلة الدرجة الرابعة. في كتابه المناظر. بينما كان يحل هذه المسألة، قام بعملية تكامل لإيجاد حجم السطح المكافئ. وقد استطاع بالاستقراء الرياضي تعميم هذه النتيجة لدوال كثيرة الحدود حتى الدرجة الرابعة وقد كان بالتالي قادرا على إيجاد صيغة عامة لتكاملات كثيرة الحدود ولكنه لم يعر للأمر أهمية لذلك في وقته.[3] بعض الأفكار في التفاضل التكاملي يمكن مشاهدتها أيضا في سيدهانتا شيروماني، وهي عبارة عن نص يعود للقرن الثاني عشر للفلكي الهندي بهاسكارا الثاني.
لم يبدأ ظهور التقدم الملحوظ في علم التكامل التفاضلي إلا مع القرن السادس عشر وفي هذا الوقت كان عمل كافاليري بطريقته الكل لا التجزيء وعمل فيرمات، ولقد بدأ بوضع الأساسيات لعلم التفاضل والتكامل الحديث. وكان لإسحق نيوتن وتورشيلي دورا هاما أيضا في توسيع هذا العلم أوائل القرن السابع عشر اللذان قدما التلميحات الأولى في وجود صلة بين التكامل والاشتقاق في الوقت الذي كان الرياضيون اليابانيون قد أسهمو في أعمال مشابهة وبشكل خاص على يد سيكي كاوا.[4] كان منها طرق إيجاد مساحات الأشكال بالتكامل، بتوسيع طريقة الاستنزاف.
نيوتن وليبنز
مثل اكتشاف النظرية الأساسية للتفاضل والتكامل الفريد من قبل إسحاق نيوتن وليبنيز تقدما عظيما في علم التفاضل والتكامل. فهي توضح العلاقة بين التكامل والتفاضل. هذه العلاقة -بدمجها مع قرينتها السهلة - الاشتقاق يمكن استغلالها لحساب التكاملات. وبشكل خاص فإن النظرية الأساسية للتفاضل والتكامل تساعد في حل مسائل أكثر تعقيدا. وبإعطاء اسم التفاضل المتناهي في الصغر فقد سمحت بتحليل دقيق لدوال متصلة. لقد أصبح هذا العمل التفاضل والتكامل الحديث، والذي استمد رمزه من عمل ليبنيز.
صياغة التكاملات
مع أن نيوتن وليبنز أوجدا طريقة نظامية للتكامل إلا أن عملهما كان يفتقر إلى درجة الدقة. فقد هاجم جورج بركلي عبارة متناهي في الصغر ووصفها بكميات الأشباح المغادرة. اكتسب التفاضل والتكامل مع تطور علم النهايات وتوطدت أركانه بفضل أوغستين لوي كوشي في منتصف القرن التاسع عشر. تم أولا صياغة التكامل بدقة باستعمال النهايات من قبل بيرنارد ريمان كما ظهرت صورة أخرى من قبل هنري لوبيغ في تأسيس نظرية القياس.
العلامة
استعمل نيوتن عمودا صغيرا فوق المتغير للإشارة إلى عملية التكامل، أو أن يضع المتغير داخل مربع. كان القضيب العمودي يلتبس مع و, والتي كان قد استعملها نيوتن للإشارة للتفاضل. كما أنه من الصعب على الطابعة التعامل مع المربع، وبالتالي لم يتم تبني هذه العلامات. الرمز الحديث للتكامل الغير محدود تم تقديمه على يد ليبنيز عام 1675 (Burton 1988، p. 359; Leibniz 1899، p. 154), كما أنه قام بموائمة رمز التكامل,:, بعد إطالته للحرف s كتمثيل لاختصار عملية الجمع sum. الشكل الحديث لعلامة التكامل المحدود استعمل لأول مرة من قبل جوزيف فوريير بإضافة حدود التكامل أسفل وأعلى الرمز السابق (Cajori 1929، pp. 249–250; Fourier 1822، §231).
الجدير بالذكر أن الرياضيات العربية التي تكتب من اليمين لليسار تستعمل الرمز المعكوس للتكامل, ![]() ، ليتماشى مع اتجاه الكتابة.(W3C 2006).
، ليتماشى مع اتجاه الكتابة.(W3C 2006).
مقدمة
تظهر التكاملات في العديد من الحالات التطبيقية. إذا اعتبرنا بركة السباحة مثلا، إذا كانت مستطيلة الشكل، من طولها، عرضها, وعمقها فمن الممكن إيجاد حجم الماء التي يمكن احتواؤها (لملئها), مساحتها السطحية (التي تغطيها من جميع الجهات), وطول حوافها (بحبل مثلا). لكن إذا كانت بيضاوية الشكل ومدورة من القعر، فإن كل هذه الكميات تستدعي التكامل. قد تكون التقريبات التطبيقية كافية في مثل هذه الأمثلة البسيطة ولكن الدقة الهندسية تتطلب قيما مضبوطة ودقيقة لهذه العناصر.
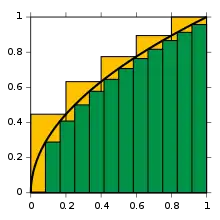
للبدء، اعتبر المنحنى بين x = 0 وx = 1, و. يكون السؤال:
- ماهي المساحة تحت الدالة f, في الفترة 0 إلى 1?
ولندعي أن هذه المساحة (حتى الآن غير معلومة) هي تكامل f. يكون الرمز لهذا التكامل هو:
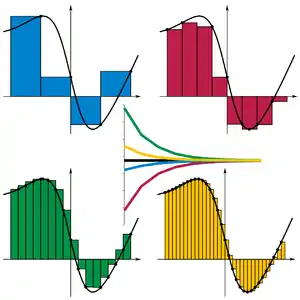
كتقريب أولي فلننظر في مربع الوحدة المعطى بالأضلاع x = 0 إلى x = 1 و nbsp;= 0 and y = f(1) = 1. مساحته هي 1 تماما. ينبغي أن تكون القيمة الحقيقية للتكامل أقل مما هي عليه. بتقليل عرض المستطيلات التقريبية يعطي نتيجة أفضل، وبالتالي عبر الفترة في خمس خطوات، باستعمال نقاط التقريب 0, 1⁄5, 2⁄5, وهكذا حتى 1. بوضع مربعا مناسبا لكل خطوة مستخدمين الارتفاع المناسب لكل قطعة منحنية، وعليه 1⁄5√, 2⁄5√, وهكذا حتى 1√= 1. وبجمع مساحات هذه المستطيلات، نحصل على تقريبا أفضل للتكاملات المقصودة,
لاحظ أننا نأخذ مجموع لقيم دوال عديدة محدودة لـ f, مضروبة في الفرق بين فترتين تقريبيتين متعاقبتين. يمكننا ملاحظة أن التقريب ما زال كبيرا. وكلما استخدمنا خطوات أكثر حصلنا على تقريبات أفضل، ولكننا لن نحصل على قيم دقيقة أبدا: بإبدال الـ5 فترات بـ12 فترة نحصل على التقريب 0.6203, وهي تقريب أفضل. مفتاح الفكرة يكمن في الانتقال من العديد من نقاط التقريب المحدودة مضروبة بقيم دالتها إلى استعمال عدد لانهائي أو خطى متناهية في الصغر. بالنسبة للحساب الحقيقي للتكامل، تكون النظرية الأساسية للتكامل هي الرابط الأساسي بين عمليات الاشتقاق والتكامل. وبتطبيقها على منحنى الجذر التربيعي,f(x) = x1/2, تقترح علينا أن نبحث عن المشتق العكسي F(x) = 2⁄3x3/2, ونأخذ ببساطة F(1) − F(0), حيث 0 و1 هي حدود الفترة [0,1].هذه حالة لقاعدة عامة، لإجل f(x) = xq, مع q ≠ −1, تكون الدالة المتعلقة والتي تدعى المشتق العكسي هي وبالتالي فإن القيمة الدقيقة للمساحة تحت المنحنى رسميا كما يلي
تعريفات منهجية
هناك عدة طرق لتعريف التكامل بشكل منهجي، لكن هذه الطرق مختلفة عن بعضها البعض في الطرق التي تسلكها. بعض هذه الاختلافات نتجت عن محاولات الرياضيين لحل حالات خاصة من المسائل التي تكون فيها المسألة غير قابلة للتكامل، وبعضها الآخر نتجت لأسباب تعليمية -كتسهيل حل المسائل-. إن أكثر تعريفين شيوعاً للتكامل هي تكامل ريمان وتكامل لوبيغ.
تكامل ريمان
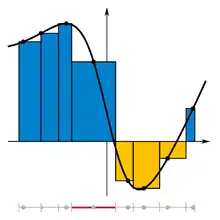
يمكن تعريف تكامل ريمان على أنها أخذ مجموع ريمان للدالة الموجودة ضمن مجال جزئها المحدد Tagged partition. فإذا كان الفترة [a,b] هي فترة مغلقة في خطها الحقيقي؛ فإن جزئها المحدد ضمن الفترة [a,b] هي سلسلة متناهية، حيث تكون:
وهذا سيجزئ الفترة [a,b] إلى n جزء ذو الفترة الجديدة [xi−1, xi]، حيث أن i يعتمد على عدد الأجزاء، كل واحد من هذه الأجزاء «تم تحديدها» بنقطة مفرِّقة ti التي تنتمي للفترة [xi−1, xi]. إذاً، تُعرّف مجموع ريمان للدالة f الموجودة ضمن الجزء المحدد من الفترة [a,b] على النحو التالي:
و بالتالي، كل حد من المجموع هي عبارة عن مساحة لمضلع لديه ارتفاع تساوي قيمة الدالة عند النقطة المفرقة للجزء المعطى، ولديه عرض تساوي طول الفترة الجزئية. فلتكنΔi = xi−xi−1 هي عرض الفترة الجزئية i; لكي يكون تشبيك هذا النوع من الأجزاء المحددة هي نفسها عرض أكبر فترة جزئية تم تشكيلها بواسطة التجزئية، التي لها القيمة القصوى i=1…n Δi. إذاً، تكامل ريمان للدالة f في الفترة [a,b] هي مساوية للقيمة S: فإذا كان جميع قيم ε > 0، ستكون جميع قيم δ > 0. وإذا كان هناك جزء محدد في الفترة [a,b] أقل من قيمة δ, ستكون:
تكامل لوبيغ للدوال غير سالبة القيمة
لتكن نعرف تكامل f بالنسبة للمقياس على أنه العدد الحقيقي الممتد حيث sup يسري على كل الدوال البسيطة التي تحقق إذا كانت E مجموعة قابلة للقياس نعرف تكامل f على E بالنسبة للمقياس على أنه العدد الحقيقي الممتد إذا تكامل f على E هو مجرد تكامل الدالة .لاحظ أن هذه الدالة غير سالبة وقابلة للقياس طالما كانت f كذلك.
خواص التكامل
من خواص التكامل (المحدد) :
- إذا كانت n مجموعة الأعداد الحقيقية وكانت قابلة للتكامل على فإن :
- إذا كانت الدالة قابلة للتكامل على الفترة فإن :
- وإذا كانت فإن:
- إذا كانت الدالة قابلة للتكامل على الفترة وكانت النقطة فإن :
- إذا كانت الدالة د قابلة للتكامل على و على هذه الفترة فإن :
- إذا كانت الدالتان قابلتين للتكامل على فإن الدالة تكون قابلة للتكامل على ويكون :
النظرية الأساسية للتفاضل والتكامل
النظرية الأساسية للتفاضل والتكامل تربط بين عملتي التفاضل والتكامل على أنهما عمليات عكسية لبعضهما، حيث انه إذا كان لدينا إقتران متصل ق(س)، قمنا بتكامله أولاً، ومن ثم إشتقاقه، فإن النتيجة النهائية هي الإقتران المتصل ق(س) نفسه.[5][6][7]
الجزء الأول من النظرية ينص على أن التكامل المحدد يمكن عكسه بالتفاضل. الجزء الثاني من النظرية يمكن الشخص من حساب تكامل محدد لدالة باستخدام أحد اشتقاقاتها العكسية غير المحدودة. هذا الجزء من النظرية لهُ أهمية كبيرة عملياً لأنه يسهل حساب التكاملات المحددة بشكل كبير.
الجزء الأول «النظرية الأولى»
افترض أن الاقتران اقتران متصل (دالة مستمرة) ذات قيم حقيقية (دالة حقيقية المستقر) معرّف على الفترة المغلقة ، وافترض أن الاقتران معرّف، كما يلي
فإن:-
- متصل على الفترة المغلقة
- قابل للإشتقاق (دالة قابلة للاشتقاق) على الفترة المفتوحة
الجزء الثاني «النظرية الثانية»
إذا كان الإقتران إقتران متصل ذات قيم حقيقية معرّف على الفترة المغلقة ، فإن:
بحيث أن، الاقتران هو أي مشتق عكسي للاقتران
بمعنى:
المراجع
- كتاب الرياضيات الصف الثالث ثانوي، الفصل الدراسي الثاني طبعة 1431-1432 هـ المملكة العربية السعودية
- Shea, Marilyn (مايو 2007)، Biography of Zu Chongzhi، University of Maine، مؤرشف من الأصل في 23 مارس 2018، اطلع عليه بتاريخ 09 يناير 2009
Katz, Victor J. (2004)، A History of Mathematics, Brief Version، أديسون-ويسلي ، ص. 125–126، ISBN 978-0-321-16193-2{{استشهاد}}: صيانة CS1: extra punctuation (link) - Victor J. Katz (1995), "Ideas of Calculus in Islam and India", Mathematics Magazine 68 (3): 163-174 [165]
- Victor J. Katz (1995), "Ideas of Calculus in Islam and India", Mathematics Magazine 68 (3): 163–174 [165–9 & 173–4]
- [وصلة مكسورة] نسخة محفوظة 30 ديسمبر 2006 على موقع واي باك مشين.
- Gregory, James (1668)، Geometriae Pars Universalis، Museo Galileo: Patavii: typis heredum Pauli Frambotti، مؤرشف من الأصل في 6 مارس 2020.
- Malet, Antoni (1993)، "James Gregorie on tangents and the "Taylor" rule for series expansions"، Archive for History of Exact Sciences، سبرنجر، doi:10.1007/BF00375656،
Gregorie's thought, on the other hand, belongs to a conceptual framework strongly geometrical in character. (page 137)
- Child, James Mark؛ Barrow, Isaac (1916)، The Geometrical Lectures of Isaac Barrow، Chicago: Open Court Publishing Company، مؤرشف من الأصل في 5 أغسطس 2016.