موتر
المُوَتِّر[1] أو المُمْتَدّ[2] (بالإنجليزية: tensor) في الرياضيات، أحد الدوال الرياضية بجانب الأعداد أو الكميات المطلقة generalized'quantity' التي لا تتميز بوحدات للقياس. يتميز الموتّر بأنه يحتوي في خواصه خواص الأعداد المطلقة scalar، والمتجهات، والمؤثرات الخطية linear operator.
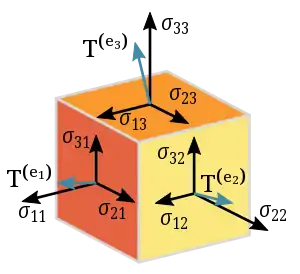
أعمدة هذه المصفوفة هي الإجهادات (القوة على كل وحدة مساحية) العاملة على الأوجه e1 و e2 و e3 للمكعب.
التاريخ
انبثق مفهوم الموتر من عمل كارل فريدريش غاوس في الهندسة التفاضلية. انظر إلى متعددة حدود متجانسة.
تعريف
يمكن للموتّر أن يكتب بدلالة الإحداثيات، أو مصفوفات قيم سلمية، لكنه يعرف على أنه مستقل عن أي إطار مرجعي.
للموتّرات أهمية كبيرة في الفيزياء والهندسة التطبيقية. ففي مجال تصوير الانْتِشار المُوَتِّر[3] Diffusion tensor imaging، يعبر الموتّر عن النفاذية التفاضلية للمركبات العضوية في الماء، مثلا أو في نسيج الدماغ.
أما أهم تطبيقات الموتّر في الهندسة التطبيقية (المدنية خصوصا) فهو موتر الإجهاد وموتّر التشوه strain tensor، وكلاهما موتّرات من الرتبة الثانية ويرتبطان بمادة خطية عامة عن طريق موتّر المرونة elasticity tensor ذو الرتبة الرابعة.
تعتبر المتجهات مثلا موتّرات من الدرجة الأولى والموتّر في حد ذاته هو ذلك الشعاع الذي نرسمه على الورقة مثلا أما الشعاع أو المتجة فما هو إلا مظهر من مظاهر الموتّر، حيث يمكننا أن نكتب الموتّر في قواعد مختلفة تعطينا إحداثيات مختلفة للمتجه.
موضوع الموترات هو موضوع فيزيائي ورياضي ولكنه ظهر في ميدان الفيزياء أولا ثم التقطه الرياضيون بعد ذلك وهذبوه ونقوه من التناقضات وصار بعد ذلك موضوعا رياضيا. وكان لألبرت أينشتاين دورا كبيرا في شهرة حساب الموترات لأنه استخدم هذا الحساب في نظريته النسبية العامة.
وفي الفيزياء توجد أنواع عديدة من الكميات، فهناك كميات قياسية وكميات متجهة ثم كميات موترة أو تنسورية. فما هو الفارق بين هذه الكميات؟ الكميات القياسية يعبر عنها برقم واحد بالإضافة إلى وحدة للقياس. فمثلا عندما نقول عن كتلة شئ أنها 3 كجم فإن ما نحتاجه هو رقم واحد وهو الرقم ثلاثة بالإضافة إلى وحدة القياس وهي الكيلوجرام. أي أن كتلة الشيء الذي أمامي هي ثلاثة أضعاف كتلة جسم قياسي يستخدم لقياس الكتل. وكذلك الحال بالنسبة للطول 3 متر أو للزمن 3 ثواني. ففي كل هذه الحالات أحتاج لرقم واحد من أجل تعيين الكمية تعيينا كاملا. ثم تأتى بعد ذلك الكميات المتجهة. وكلمة متجه أو vector تعنى باللغة اللاتينية سائق أو أنه يوجه في اتجاه معين. وهذا النوع من الكميات لا يمكن وصفه عن طريق رقم واحد. ولكني أحتاج لأكثر من رقم لوصف الكمية التي أمامي. مثال على ذلك هي الإزاحة: فإنني إذا طلبت منك أن تزيح كوبا من الماء موضوعا فوق منضدة فارغة مسافة 50 سم فستسألني في أي اتجاه ينبغى أن تزيحه للإمام؟ للخلف؟ لليمين؟ لليسار؟ فالإزاحة تحتاج بجانب مقدار المسافة وهو 50 سم "رقم آخر" يعبر عن الاتجاه. وقد يكون هذا الرقم مثلا عبارة عن "الزاوية | اللتى يصنعها الاتجاه المقصود مع اتجاه الشمال الجغرافي مقاسة في اتجاه دوران عقرب الساعة. فعندما أقول مثلا أن عليك أن تحرك الكوب مسافة 50 سم بالزاوية 90 درجة فإنني أعني بذلك أن تحرك الكوب 50 سم في اتجاه الشرق. ولكن عموما فإن المتجهات يتم التعبير عنها في الإحداثيات الكارتيزية بمجموعة أرقام يساوي عددها عدد الأبعاد في الفضاء الموجود. ويعبر عن المتجه رياضيا بصورة مصفوفة ذات عمود واحد.
كلمة موتر هي مشتقة من الكلمة الإنجليزية Tension بمعنى شدة أو توتر. ولذلك تأتى الترجمة العربية التي قد تبدو غريبة بعض الشئ الموترات. والموترات هي متجهات فائقة. بمعنى كما أن المتجه مجموعة من الأعداد أو الكميات القياسية فإن الموتر هو مجموعة من المتجهات. مثال: عندما أطلب منك أن تزيح عصا طويلة موجودة فوق الطاولة في اتجاه ما. فإن متجه واحد لن يكفي لوصف هذه العملية. لماذا؟ لأن كوب الماء يمكننا تخيله نقطة واحدة. أما في حالة العصا فإنها قد لا تحافظ بالضروة بعد إزاحتها على نفس الاتجاه التي كانت تأخذه قبل الإزاحة. فمثلا قد تكون العصا تشغل في البداية اتجاه الشمال-الجنوب ولكنها بعد الإزاحة ينبغى أن تأخذ اتجاه الشرق-الغرب.
ومن هنا فان متجها واحدا لايكفي لوصف هذه العملية بل نحن في حاجة إلى مجموعة من المتجهات. ويعبر عن عن الموترات بصورة مصفوفة.
ثم أن هناك درجة أعلى من الموترات وهي الموترات الفائقة وهي بدورها عبارة عن مجموعة من الموترات لوصف عملية ما. على سبيل المثال، إذا طلبت منك ازاحة عصا طويلة موضوعة على منضدة مسافة ما. وكما رأينا أن هذه العملية تحتاج لموتر كما سبق ووضحنا. فإذا أضفت أن العصا بعد إزاحتها لن تحافظ على استقامتها بل إنها ستأخذ شكلا مقوسا ما فإننا نرى أن موترا واحد لن يكفي لوصف هذه العملية بل إننا نحتاج إلى مجموعة من الموترات أو موتر فائق.
وهكذا فإننا نرى أنه لا توجد نهاية لهذه العملية وبإمكاننا أن نعرف موترات فوق الفائقة وهكذا إلى مالانهاية. وفي بعض الكتب نجد أن الكميات القياسية يتم توصيفها بأنها موترات من الدرجة صفر أما المتجهات فهي موترات من الدرجة الأولى ثم إن الموترات العادية هي من الدرجة الثانية أما الموترات الفائقة فهي من الدرجة الثالثة وهكذا.
إن الموتر في الفيزياء هو كمية فيزيائية حقيقية وبالتالي فهي تحافظ على قيمتها بغض النظر عن محاور الإسناد المستخدمة لوصف هذه الكمية. ولهذه النقطة دور مهم في النسبية العامة. حيت أن جميع القوانين الفزيائية تحافظ على صورتها بغض النظر عن محاور الإسناد.
أهمية الموترات
الهندسة التحليلية أو الهندسة الجبرية تقوم على تحويل المفاهيم الهندسية كالنقطة والخط والمستوى إلى معادلات جبرية متجهة. أي أنها المتجهات تلعب هنا الدور الأكبر في وصف الهندسة. ثم تأتي بعد ذلك الهندسة التفاضلية التي تعبر عن هندسات أعقد من الهندسة الاقليدية كهندسة ريمان. وهنا يلعب الموتر دورا كبيرا. فتظهر الحاجة إلى معلومات متطورة في حساب المتجهات وحساب الموترات والتفاضل والدوال بدلالة أكثر من متغير وتفاضل هذه الدوال تفاضل جزئي أو تفاضل كامل.
للموترات دور هائل في الفيزياء الحديثة. فأي كمية أو أي قانون فيزيائي سليم يجب أن يأخذ صورة معادلات تنسورية بشكل أو بآخر. وقد يكون الموتر من الدرجة صفر أو واحد أو اثنين أو ثلاثة أو أعلى من ذلك.
تعميمات
الموترات في أبعاد غير منتهية
أساسيات
المراجع
- البنك الآلي السعودي للمصطلحات (باسم). [وصلة مكسورة] نسخة محفوظة 30 ديسمبر 2017 على موقع واي باك مشين.
- معجم المصطلحات على موقع مجمع اللغة العربية بالقاهرة. [وصلة مكسورة] نسخة محفوظة 04 مايو 2015 على موقع واي باك مشين.
- سلسلة مكتبة الأشعـة والتصـوير الطبـي ، التَّصْويرُ بالرَّنينِ المِغْناطيسِيّ magnetic resonance imaging MRI ، ماهر محمدى يس - خبير تقني الأشعة والتصويرالطبي ، الطبعة الرابعة 2012 CAIRO – EGYPT ، مرجع في الرنين المغناطيسي باللغة العربية مع المحافظة على المصطلح الطبي باللغة الإنجليزية – مبسط شامل كل مايخص التصوير بالرنين المغناطيسي نسخة محفوظة 04 مارس 2016 على موقع واي باك مشين.
- بوابة رياضيات
- بوابة الفيزياء