قاعدة لايبنتز للتكامل

قاعدة لايبنتز للتكامل هي قاعدة رياضياتية في حساب التفاضل والتكامل سميت تيمنا بغوتفريد لايبنتز، والتي تقول أن كل تكامل على شاكلة:

التفاضل والتكامل
جزء من سلسلة مقالات حول
* المبرهنة الأساسية نهايات الدوال استمرارية مبرهنة القيمة المتوسطة مبرهنة رول تفاضل وتكامل كسري
حساب التفاضل اشتقاق حساب المتغيرات تفاضل ضمني مبرهنة تايلور معدلات مرتبطة متطابِقات قواعد قاعدة القوة قاعدة الضرب قاعدة ناتج القسمة قاعدة التسلسل قاعدة لايبنتز للتكامل
حساب التكامل تكامل قائمة التكاملات تكاملات معتلة تكامل ريمان تكامل متعدد التكامل بواسطة التجزئة الأقراص الطبقات الأسطوانية التعويض التعويضات المثلثية الكسور الجزئية تغيير الرتب
حساب المتسلسلات متسلسلة هندسية (حسابية هندسية) متسلسلة متناسقة متسلسلة متناوبة متسلسلة قوى متسلسلة ذو الحدين متسلسلة تايلور اختبارات التقارب اختبار الحد النوني اختبار النسبة اختبار الجذر اختبار التكامل للتقارب اختبار المقارنة اختبار مقارنة النهاية اختبار متسلسلة متناوبة اختبار التكثف لكوشي اختبار دركليه اختبار أبيل
حساب المتجهات تدرج تباعد دوران (إلتواء) لابلاسي مبرهنة التدرج مبرهنة غرين مبرهنة ستوكس مبرهنة التباعد مبرهنة كلفن-ستوكس (مبرهنة الدوران)
حساب متعدد المتغيرات حسبان المصفوفات اشتقاق جزئي تكامل متعدد تكامل خطي تكامل سطحي تكامل حجمي جاكوبي
بوابة رياضيات

$\int _{a(x)}^{b(x)}f(x,t)\,dt,$

حيث أن $-\infty <a(x),b(x)<\infty$ مشتقته بالشكل التالي:

{\frac {d}{dx}}\left(\int _{a(x)}^{b(x)}f(x,t)\,dt\right)=f{\big (}x,b(x){\big )}\cdot {\frac {d}{dx}}b(x)-f{\big (}x,a(x){\big )}\cdot {\frac {d}{dx}}a(x)+\int _{a(x)}^{b(x)}{\frac {\partial }{\partial x}}f(x,t)\,dt,

حيث آن المشتق الجزئي يدل على أن ما داخل التكامل يمكن الأخذ به عندما يكون المتغير f(x, t) x يعتبر في اتخاذ مشتق.[1] لاحظ أنه إذا كان كلا من $a(x)$ و $b(x)$ ثوابت، بمعنى أنّ $a(x)\equiv a$ و $b(x)\equiv b$ ، فسنحصل على التعبير التّالي:

${\frac {d}{dx}}\left(\int _{a}^{b}f(x,t)\,dt\right)=\int _{a}^{b}{\frac {\partial }{\partial x}}f(x,t)\,dt.$

حالة الأبعاد الثلاثة التي تعتمد على الزمن

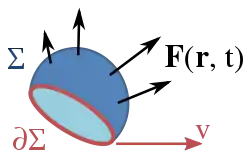
الشكل 1: حقل متجه F(r, t) محددة في جميع أنحاء الفضاء, سطح Σ يحدها منحنى ∂Σ تتحرك مع سرعة v على حقل دمج.

ان قاعدة لايبنتز للأبعاد الثنائية هي:[2]

{\frac {d}{dt}}\iint _{\Sigma (t)}\mathbf {F} (\mathbf {r} ,t)\cdot d\mathbf {A} =\iint _{\Sigma (t)}\left(\mathbf {F} _{t}(\mathbf {r} ,t)+\left[\nabla \cdot \mathbf {F} (\mathbf {r} ,t)\right]\mathbf {v} \right)\cdot d\mathbf {A} -\oint _{\partial \Sigma (t)}\left[\mathbf {v} \times \mathbf {F} (\mathbf {r} ,t)\right]\cdot d\mathbf {s} ,

حيث أن:

F(r, t) هو حقل متجه في موقف المكاني r في الوقت t,

Σ هو سطح متنقل في مساحة ثلاثية يحدها منحنى مغلق ∂Σ ،

dA هو متجه عنصر من سطح Σ،

ds هو متجه عنصر من منحنى ∂Σ،

v هي سرعة الحركة من المنطقة Σ،

∇⋅ هو متجه الاختلاف،

× هو متجه عبر المنتج،

إن ضعف التكامل هي التكاملات السطحية على سطح Σ و خط متكامل على إحاطة منحنى ∂Σ.

الأبعاد العليا

يمكن تمديد قانون ليبنيز ليشمل تكاملات في أبعاد متعددة. تسمى في حالة البعدين والثلاثة بمجال ديناميات السوائل كما في نظرية رينولدز للنقل:

${\frac {d}{dt}}\int _{D(t)}F({\vec {\textbf {x}}},t)\,dV=\int _{D(t)}{\frac {\partial }{\partial t}}F({\vec {\textbf {x}}},t)\,dV+\int _{\partial D(t)}F({\vec {\textbf {x}}},t){\vec {\textbf {v}}}_{b}\cdot d\mathbf {\Sigma } ,$

انظر أيضًا

المراجع

Protter, Murray H.؛ Morrey, Charles B., Jr. (1985)، "Differentiation under the Integral Sign"، Intermediate Calculus (ط. Second)، Springer، ص. 421–426، ISBN 0-387-96058-9.
Flanders, Harly (يونيو–يوليو 1973)، "Differentiation under the integral sign" (PDF)، الرياضيات الأمريكية الشهرية، 80 (6): 615–627، doi:10.2307/2319163، JSTOR 2319163، مؤرشف من الأصل (PDF) في 20 سبتمبر 2018.

مزيد من القراءة

Frederick S. Woods (1934)، Advanced Calculus (ط. New)، Ginn and Company، ASIN B0006AMNBI.
Frederick S. Woods (1926)، Advanced Calculus (ط. 1st)، Ginn and Company، ASIN B00085L67S.
David V. Widder (يوليو 1990)، Advanced Calculus (ط. New)، Dover Publications Inc.، ISBN 978-0-486-66103-2.

مواضيع التفاضل والتكامل
ما قبل حساب التفاضل والتكامل ^{[الإنجليزية]}	مبرهنة ذي الحدين دوال خطيَّة مُستمِرة مُقعَّرة العاملي فرق محدود المتغير الحر والمتغير المقيد تمثيل الدالة البياني ميل المستقيم راديان مبرهنة رول القاطع المماس
النهايات	صيغة غير مُحدَّدة نهاية دالة وحيدة الجانب ^{[الإنجليزية]} نهاية متتالية درجة التقريب
حساب التفاضل	مُشتَق تفاضلي ^{[الإنجليزية]} معادلة تفاضلية مؤثر تفاضلي مبرهنة القيمة المتوسطة تدوين التفاضل ^{[الإنجليزية]} لايبنز نيوتن ^{[الإنجليزية]} قواعد التفاضل الخطيَّة الرفع إلى أُس السلسلة لوبيتال الضرب قاعدة لايبنيز العامة ناتج القسمة تقنيات أخرى الدوال العكسية اللوغاريتم المعدلات المرتبطة نقاط الثبات اختبار المشتق مبرهنة القيمة المُتَّطرفة ^{[الإنجليزية]} النقاط الحرجة تطبيقات أُخرى طريقة نيوتن لإيجاد الجذور سلسلة تايلور
حساب التكامل	المبرهنة الأساسية مُشتَق التكامل ثابت التكامل بالتجزئة بالتعويض مُثلثي أويلر ^{[الإنجليزية]} فايرشتراس ^{[الإنجليزية]} تربيعي ^{[الإنجليزية]} شبه المنحرف مُشتَق عكسي طول القوس الحجوم بالأقراص بالطبقات الأسطوانية
حساب المتجهات	مشتق اتجاهي المؤثرات دوران تباعد تدرج لابلاس مبرهنات رئيسة التدرُّج التباعد غرين كلفن وستوكس
حساب التفاضل والتكامل متعدد المتغيرات	مبرهنة التباعد حساب المصفوفات حساب هندسي ^{[الإنجليزية]} ياكوبية هيسية معامل لاغرانج ^{[الإنجليزية]} تكاملات خط سطح حجم متعدد مشتق جزئي مواضيع مُتقدِّمة أشكال تفاضلية مشتق خارجي مبرهنة ستوكس المُعمَّمة حساب المُوتِّر
المتتاليات والسلاسل	متتالية حسابية هندسية ^{[الإنجليزية]} أنواع السلاسل متناوبة ذات حدين فورييه هندسية متناسقة قوى تايلور متداخلة اختبارات التقارب أبيل ^{[الإنجليزية]} السلاسل المتناوبة ^{[الإنجليزية]} كوشي للتكثيف ^{[الإنجليزية]} المقارنة المباشرة ^{[الإنجليزية]} دركليه ^{[الإنجليزية]} التكامل ^{[الإنجليزية]} مقارنة النهايات ^{[الإنجليزية]} النسبة الأصل ^{[الإنجليزية]} الحد النوني
دوال وأرقام مُميَّزة	أعداد برنولي ثابت أويلر دالة أسية لوغاريتم طبيعي تقريب ستيرلينغ
تاريخ التفاضل والتكامل	شخصيات تايلور ماكلورين لايبنتس نيوتن أويلر مفاهيم تسوية ^{[الإنجليزية]} المتناهيات في الصغر التدفق قانون الاستمرارية ^{[الإنجليزية]} عمومية الجبر ^{[الإنجليزية]} كتب طريقة المبرهنات الميكانيكية طرق التدفق
قوائم	قواعد التفاضل تكاملات الدوال اللوغاريتمية الأسية المثلثية العكسية القواطع ^{[الإنجليزية]} المُكعَّبة ^{[الإنجليزية]} الزائدية العكسية الكسرية غير الكسرية النهايات
مواضيع متنوعة	الانحناء هندسة تفاضلية للمنحنيات للسطوح ^{[الإنجليزية]} صيغة أويلر وماكلورين بوق جبريل إثبات أن 22/7 أكبر من π مسألة ريغيومونتانوس للزاوية العظمى ^{[الإنجليزية]} مجسم شتاينميتز ^{[الإنجليزية]}
تصنيف • كومنز بوابة رياضيات • بوابة تحليل رياضي • بوابة هندسة رياضية

بوابة تحليل رياضي
بوابة رياضيات

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.